High-Density Graphs

Due to one of the more unfortunate flukes in the history of mathematics, collections of objects that consists of points and connections are also called graphs.

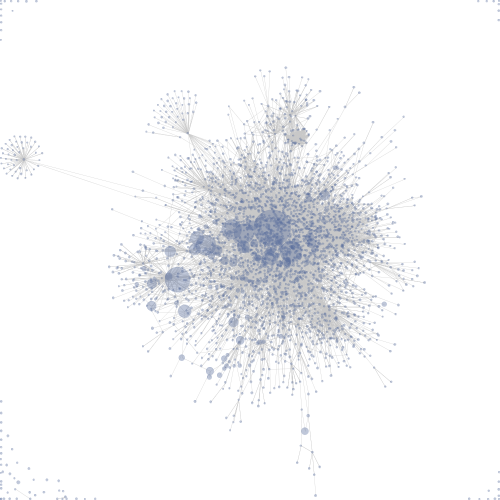
These kinds of graphs generally look like this:

network-graph

Force Directed Spring Layout of Wiki data, taken from Wikipedia.

Each dot above represents a wiki-page, each line represents a connection between the pages.

Graphs are useful in seeing, in the abstract, the relationships between objects or data points, especially when the type and number of connections are important.
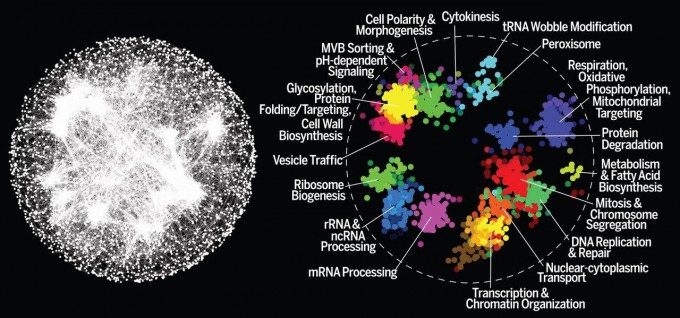
For example, the graph below represents every interaction between every gene in the yeast species Saccharomyces cerevisiae.

yeast-graph

Left: A Node and Edge Graph representation of a yeast genome. Right: important clusters of genes. Photo credit.

While interesting, you have surely noticed that both graphs above are very busy in the middle. Something similar happens if you explore the Panama Papers/Offshore Leaks Dataset — the graph of connections gets busy, quick.

The fact that most graphs become hard to understand due to the number of overlapping connections in the center of the graph can be an issue for understanding how entities relate to each other, which was the whole point of using a graph in the first place.
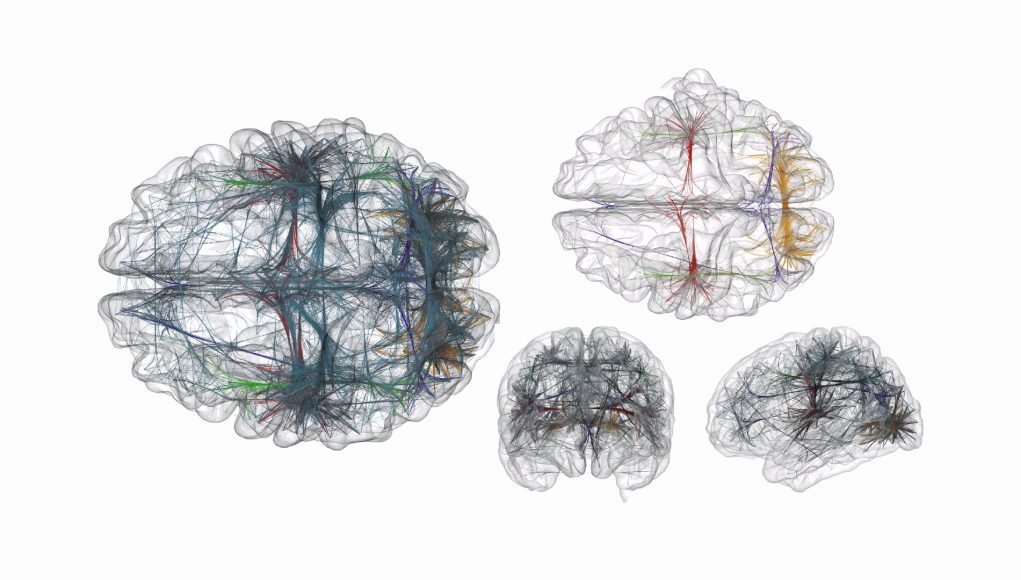
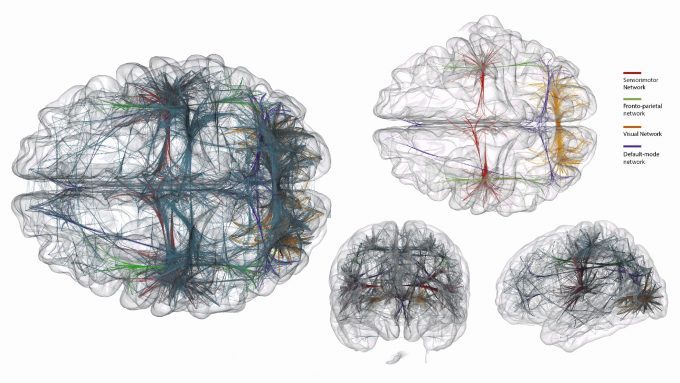
As you might imagine, three-dimensional graph visualization allows for much more breathing room:

brain-connection-visualization

A three-dimensional graph visualization of different connected networks in the brain. Photo credit.

However, notice that these visualizations also suffer from the busy-ness problem; even though the authors are using an algorithm to ‘bundle’ the connecting lines together, it is still hard to figure out what exactly is going on. Imagine, however, if you were able to fly into the middle of each of those brains and rapidly change the size and scale of the brain you were now standing the middle of it – the data would be much easier to understand.

Providing Context

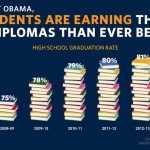
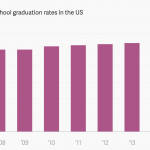
Compare the following charts:

Both of these charts use the same underlying data. The left chart was named one of the most misleading charts of 2015.

I submit that while the chart above (or the others in the linked Quartz article) is misleadingly presented, it is misleading to present it as a static image. Being able to explore and change the data’s size, shape and scale can prevent data from being misleading, because the context is baked into the experience.

SEE ALSO
'Big Data VR Challenge' $20,000 Grand Prize Winner Revealed by Epic Games and Wellcome Trust

One of the biggest advantages of using virtual reality to visualize information is that there is no point in sharing just a static VR representation; every VR representation is also automatically an experience. What this means is that the viewer can explore it at her or his will.

VR to the Rescue

While VR data tools are in their nascent stages, here are three examples that combine most of what I’ve mentioned so far.

CalcFlow

The first is CalcFlow a tool developed in concert with the UCSD math department for visualizing 3D math concepts. Currently, it is set up a series of interactive demos that allows a person to get an intuitive understanding of a double integral or the Navier-Stokes equation. You can experience some of the advantages of VR I’ve identified in this piece in each demo: the ability to change scales and “walk around” the data means that the data it is easier to understand. The experiential nature of the demo means the user can make adjustments on the fly and see how it changes the result in multiple dimensions.

DeathTools

DeathTools takes data visualization from abstract numbers into a real, tangible world that we understand in a way fundamentally different than figures and graphs. The experience shows the accumulated body count of recent Middle Eastern conflicts. Instead of a bar chart, you’re literally standing among rows of body bags that accurately represent the number of deaths.

As DeathTools creator Ali Eslami puts it:

One of the pieces that is missing in our knowledge base is the ability to perceive Big Numbers. We have trouble understanding and accepting mass death. For example, numbers like 1; 2; 14; 20; 50, are all quantities that we encounter quite frequently and therefore we’re able to rationalize them with a representative mind model. But then we get to numbers like 1,000; 10,000; 20,000. These numbers become increasingly difficult to conceptualize, but we can still grasp the general meaning of such numbers using visual models of large scale things we encounter often in our little realities.

Kineviz

Lastly, we’ve been working on a VR-enabled, 3D graph exploration tool here at Kineviz. It’s designed to solve some issues around high-information-density and allowing users to intuitively experiences meaningful differences in data. Take a look for yourself:

The major advantages of VR is that it can be used to make perceiving differences in data easier, less dense, and more intuitive. VR also forces data representation to be experiential, which means that it’s much harder to alter the representation of the data to fit a pre-defined story. Finally, VR allows a person to rapidly change the scale of what one is looking at in a way that utilizes one’s spatial awareness and allows the perception of scales of data that are otherwise nearly impossible to imagine.
1
2
Newsletter graphic

This article may contain affiliate links. If you click an affiliate link and buy a product we may receive a small commission which helps support the publication. More information.


Road to VR
  • Steven Swanson

    Great article on some of the basics of data viz and how VR can uniquely expose patterns and meaning.

  • evostars

    i would love to see the complex real magnetic field including phi spirals and bloch wall interactions in VR

    • Ryan Shearer

      Not exactly the same but have you seen ferrofluid? prity cool stuff.

  • Fred

    Great thoughts on better visualization in 3D and easier scaling, but imo this one extra spatial dimension is just a starter for the real benefits of better understanding and analyzing data with VR. It is a very transitional approach, but understandable to come from a “vizualization company” and a scholar in cognitive science. Hearing, feeling, yes even tasting (just do a search for “datagastronomification”) will add extra sensory dimensions and allow for much higher data density, ranges, real-time changes to be analyzed. Or you just “feel” something is missing or should be there. In many cases assisted by AI and no need (sometimes even better) for a trained domain expert but can be tried by the user him- or herself, first. The other benefit I miss in this article is collaboratively “experiencing” data in VR: think of the Startrek Holodeck-like stuff that is becoming real now. That will change the game for good and virtual reality will be quite disruptive for this domain too, when flat screens, mouse & keyboard are finally gone as the main HCI.

    • Ryan Shearer

      Well said, the ability to possibly develop Intuition from extra sensual inputs from data is especially interesting.

  • taparat

    Great article – note that Eslami’s experience is called Death Tolls, a far more sensible name than the misprint “Death Tools” which this article repeats twice.

    • benz145

      Ha wow, thanks for pointing this out. Fixing now.

  • Waldo

    Data visualization in VR is with out a doubt more expressive and deeper then we can ever get on a 2D screen. Since my job revolves around data and visualization for compliance warnings, I can not see my users in a VR environment looking at where they are now and where they are heading while they assign duties to their teams.

    Yet with the above stated, I do see where AR would be the best fit for this process and others where decisions are relevant to visualizations and large data sets while at the same time allowing for collaboration in the office environment.

    If a company would start developing these frameworks in VR now, they would be well on their way to successful AR implementation in the near future.

    So I would suggest it is probably time for big business to start taking VR as a serious methodology and extension to their present infrastructure so when VR and AR become some what equivalent on the the technology side and start merging together, companies who have taken the time and money to invest in VR will reap the benefits of AR with little change I their aforementioned VR visualization efforts.

    Of course this is my opinion only and I am sure others have theirs as well. So I put this forth as simply an idea for others to think about. Personally I know this is the road map I am going to pursue as AR tech moves forward and the lines between VR and AR begin to bluer.

    Regards

  • Great article! My team has been working hard on a platform to truly visualize complex datasets in VR and today we launched our closed beta and free demo on steam! I would love to hear feedback from the VR community!

    http://store.steampowered.com/app/551960/ https://uploads.disquscdn.com/images/139d8103f8ba55f2f6ca07dd1772c43cea8660277d248c4776159b98b1bfaa4a.png

  • TheMediaman1

    Fred, Evastars & others hit the mark. The article made me think, not necessarily due to an entirely new perspective, but for the free thought in visualization. —– Unclear depiction is a problem in 2 dimensions as well as 3, in real, virtual or mixed reality, etc., but VR does provide a thought-provoking opportunity. —- “Uninspiring” depiction can also have even greater consequences, as can depiction or manipulation “inefficiency” (as inferred but not entirely explored) or over-reliance on merely static graphical depiction or even limiting “visualization” to a single mode depiction. —- Thanks for inspiring me to think and providing free-thought examples to guide the way..Very nice.